내가 지난 7년간 엔지니어로 일하면서 배운 것 (2)
1985년, 미국 노스캐롤라이나 대학교 지리학과 졸업생의 평균 초봉은 무려 10만 달러였다. 2025년 환율 기준으로 약 1억 4천만 원에 달하는 금액이다. 어떻게 이런 수치가 나왔을까? 그 이유는 바로 NBA 전설 ‘마이클 조던’이 해당 학과 출신이었기 때문이다.
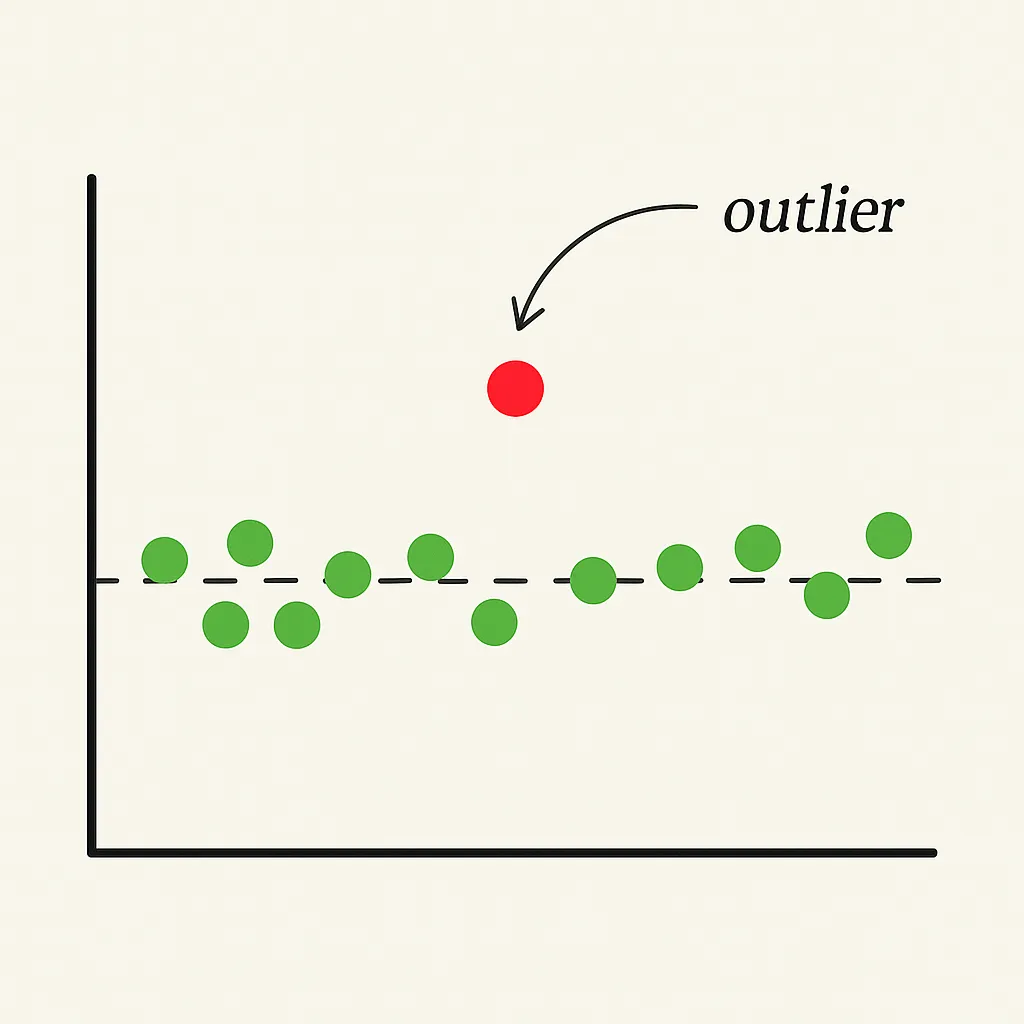
이 사례는 우리가 흔히 사용하는 평균값(Mean)이 얼마나 쉽게 왜곡될 수 있는지를 보여주는 대표적인 예다. 통계에서 평균은 하나의 중심값이지만, 극단적인 값(Outlier)이 끼어들면 전체 의미를 흐릴 수 있다.
엔지니어로 일하며 내가 자주 떠올리는 또 다른 기초 통계 개념은 바로 중앙값(Mode) 과 최빈값(Median) 이다.
왜곡된 평균값, 현실적인 중앙값
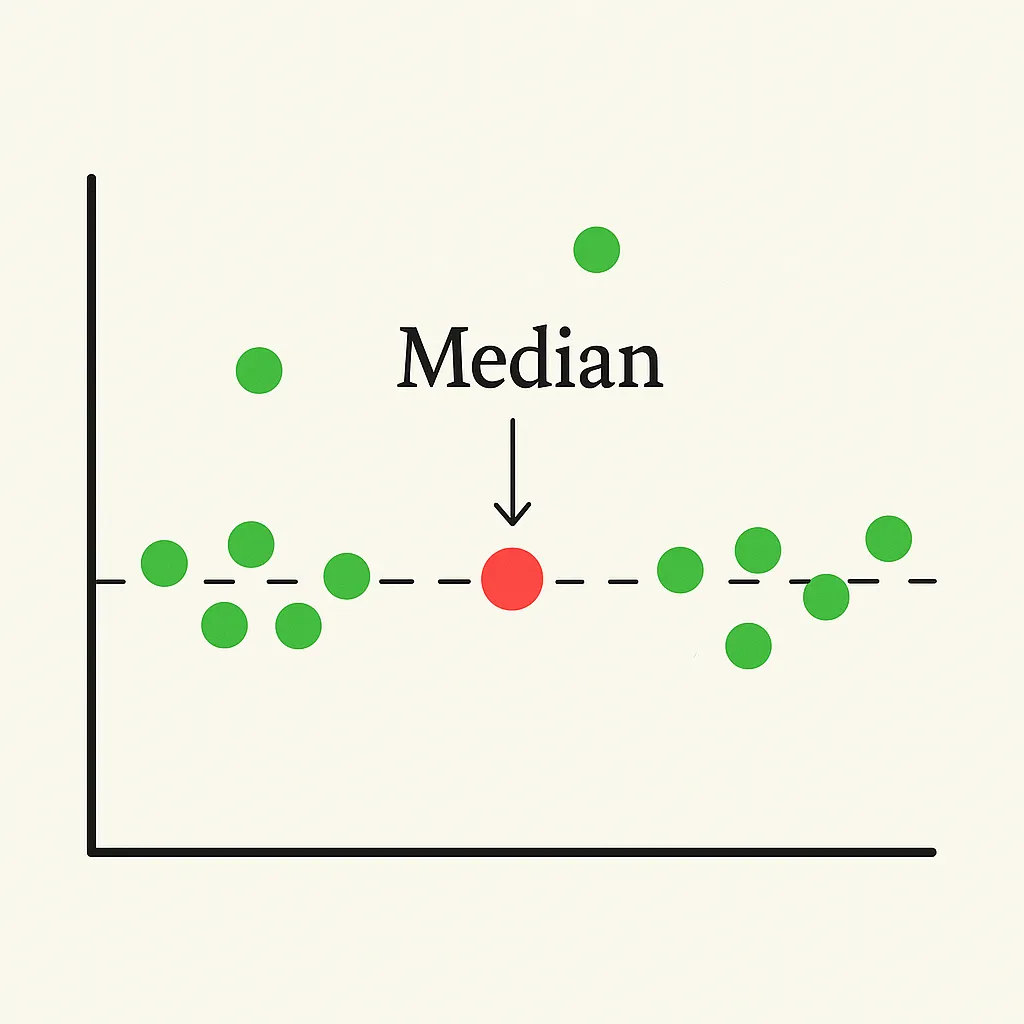
고등학교 때 배운 표준편차와 Z-스코어는 이런 왜곡을 보완해주는 도구지만, 실무에서 이들을 매번 적용하기란 번거롭다. 그럴 땐 중앙값이 훌륭한 대안이 된다.
예를 들어, 마이클 조던을 포함한 연봉 데이터에서 중앙값을 썼다면, 한 명의 아웃라이어가 전체 값을 왜곡하지 않았을 것이다. 중앙값은 정렬된 데이터의 ‘중간’에 있는 값이기에, ‘나는 전체 중 어디쯤인가?’를 판단할 때 가장 현실적인 기준점이 된다.
다수가 선택한 기준, 최빈값
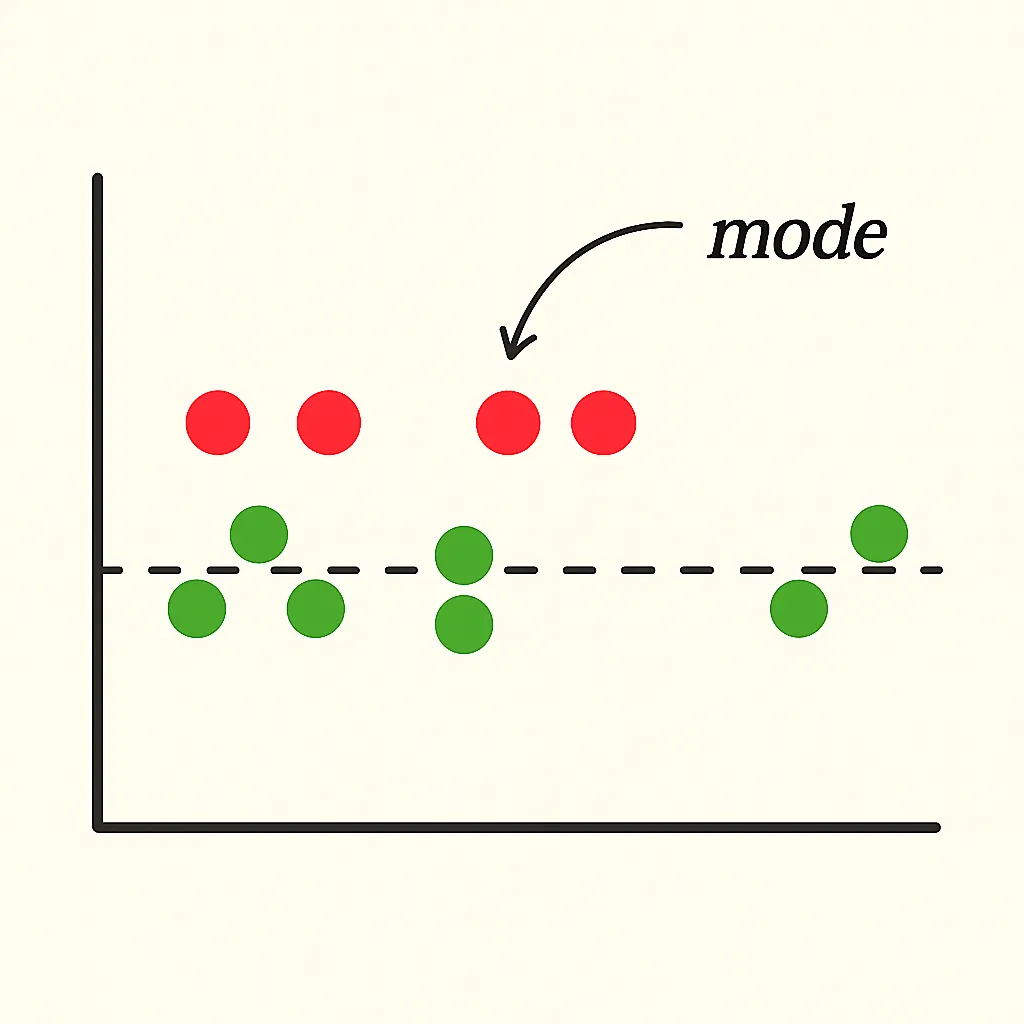 그렇다면 최빈값은 언제 유용할까? 배달 앱을 켜고 주문 내역을 살펴보자. 자주 먹는 메뉴는 어떤 기준으로 선택될까? 별점이나 리뷰보다, 반복 주문된 메뉴가 실질적인 만족도를 보여주는 경우가 많다. 이처럼 최빈값은 다수가 반복 선택한, 공감의 기준점이 된다.
그렇다면 최빈값은 언제 유용할까? 배달 앱을 켜고 주문 내역을 살펴보자. 자주 먹는 메뉴는 어떤 기준으로 선택될까? 별점이나 리뷰보다, 반복 주문된 메뉴가 실질적인 만족도를 보여주는 경우가 많다. 이처럼 최빈값은 다수가 반복 선택한, 공감의 기준점이 된다.
그렇다면 평균은 쓸모없을까?
물론 아니다. 평균값은 왜곡될 수 있지만, ‘전체적인 분포를 요약하고, 공정함을 설계하는 기준점’으로는 여전히 강력한 도구다. 예를 들어 팀원에게 맨먼스(M/M)가 명확한 업무를 고르게 분배하거나, 코드 리뷰나 온콜 로테이션처럼 반복 업무를 팀원에게 고르게 나눌 때 평균은 빠르게 기준을 제시해준다.
마지막으로 팀 생산성을 수치로 요약할 때, 즉 개별 성과가 아닌 전체 팀의 평균 속도를 보면 무리나 과부하를 조정하기 쉬워지기도 하므로 여전히 쓸모가 있다.
마무리
기초 통계는 엔지니어의 무기다. 엔지니어링 세계에는 완벽한 해법, Silver Bullet이 존재하지 않는다. 하지만 평균값, 중앙값, 최빈값처럼 단순한 기초 통계는 문제 해결의 방향을 제시해주는 현실적인 도구다.
상황에 맞는 통계 지표 하나만 잘 골라도, 머신러닝, LLM보다 빠르고 직관적인 인사이트를 얻을 수 있다. 꼭 어려운 방법만이 복잡한 문제의 해가 아닐 수 있다. 기초통계가 튼튼한 엔지니어의 판단은 간결하고 명료하다. 그게 좋은 엔지니어가 아닐까.